Διαδικασίες τρισδιάστατης αποτύπωσης

Εισαγωγή

Η συλλογή τρισδιάστατων δεδομένων με κάποιο σύστημα σάρωσης είναι μόνο η αρχή μιας ιδιαίτερα σύνθετης διαδικασίας. Τα βήματα που ακολουθούνται, αποσκοπούν στην αποτελεσματική χρήση των δεδομένων που παρέχουν οι σαρωτές.

Στην Εικόνα 57(α) περιγράφεται η σειρά εργασιών από τη στιγμή της αποτύπωσης των δεδομένων έως και της τελικής οπτικής αναπαράστασης του τρισδιάστατου μοντέλου. Η διαδικασία επεξεργασίας των δεδομένων διαχωρίζεται σε πέντε βασικά βήματα [82]:

• προ-επεξεργασία
• ενοποίηση τμηματικών σαρώσεων
• μετατροπή σε πολυγωνικό πλέγμα
• μετά-επεξεργασία
• επεξεργασία υφής

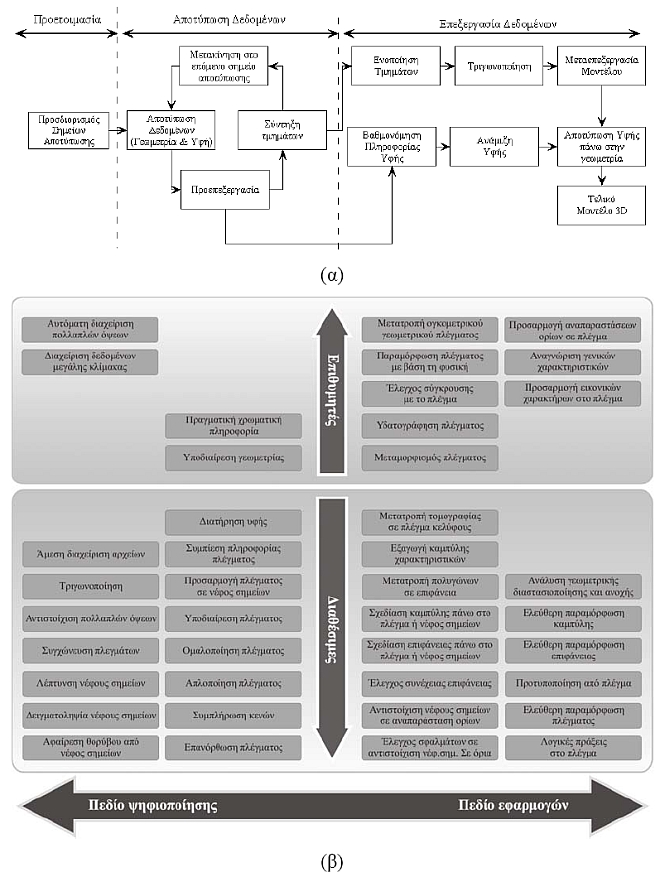
Εικόνα 58. (α) Γενικό διάγραμμα διαδικασιών δημιουργίας 3D μοντέλου, (β) συνοπτική παρουσίαση διαθέσιμων και επιθυμητών διαδικασιών επεξεργασίας δεδομένων τρισδιάστατης ψηφιοποίησης

Στην Εικόνα 58(β) παρουσιάζονται συγκεντρωμένες όλες οι (μέχρι σήμερα) διαθέσιμες αλλά και επιθυμητές (όχι ακόμη διαθέσιμες) διαδικασίες που εμπλέκονται στην επεξεργασία δεδομένων που προκύπτουν από την τρισδιάστατη ψηφιοποίηση τόσο κινητών πολιτιστικών αντικειμένων όσο και ακίνητων μνημείων και χώρων.

Στο παρόν κεφάλαιο γίνεται μια ανάλυση όλης της διαδικασίας παραγωγής τρισδιάστατων μοντέλων με τη χρήση τρισδιάστατων σαρωτών. Αναλύονται τα ειδικά προβλήματα που παρουσιάζονται σε ψηφιοποιήσεις αντικειμένων πολιτιστικής κληρονομιάς καθώς και οι δυσκολίες της συλλογής δεδομένων. Ο διαχωρισμός που γίνεται στις διαδικασίες αλλά και η περιγραφή τους μπορεί να μην συμβαδίζει με όλες τις διαθέσιμες μεθόδους ψηφιοποίησης. Ως εκ τούτου τα βήματα της διαδικασίας θα πρέπει να ληφθούν υπόψη ως ένα γενικευμένο διάγραμμα ροής εργασιών που μεταβάλλεται ανάλογα με την υιοθετημένη μεθοδολογία αποτύπωσης.

Συνολικά, τα βήματα μιας διαδικασίας ψηφιοποίησης είναι τα εξής:

• Σύλληψη γεωμετρικών δεδομένων
• Προ-επεξεργασία γεωμετρικής πληροφορίας
• Φιλτράρισμα του θορύβου στο νέφους σημείων
• Ομαδοποίηση και οργάνωση των δεδομένων
• Ευθυγράμμιση και ενοποίηση των τμηματικών σαρώσεων
• Δημιουργία πολυγωνικού πλέγματος (meshing)
• Απλοποίηση του πολυγωνικού πλέγματος
• Απαλοιφή γεωμετρικών ασυνεχειών
• Δημιουργία υφής

Τα βήματα αυτά αναπτύσσονται στο Μέρος αυτό της Μελέτης και στις παραγράφους που ακολουθούν.

 

Σύλληψη γεωμετρικών δεδομένων

Το πρώτο βήμα, είναι η σύλληψη των γεωμετρικών δεδομένων ενός αντικειμένου με κάποιον σαρωτή. Ο τρόπος εκτέλεσης της συγκεκριμένης διαδικασίας εξαρτάται σε μεγάλο βαθμό από τον τύπο του σαρωτή αλλά και τις τεχνικές του προδιαγραφές (π.χ. ταχύτητα αποτύπωσης, φορητότητα, κ.α.).

Οποιαδήποτε και αν είναι, όμως, η μέθοδος σάρωσης που θα εφαρμοσθεί η διαδικασία καταλήγει σε μια σειρά από τμηματικές σαρώσεις. Οι πολλαπλές σαρώσεις οφείλονται στο γεγονός ότι τα περισσότερα συστήματα σάρωσης απαιτούν την αποτύπωση δεδομένων από διαφορετικές γωνίες, έτσι, ώστε νακαλύψουν όλες τις επιφάνειες του αντικειμένου.

Συνηθισμένο πρακτική για κινητά αντικείμενα είναι η χρήση ενός περιστρεφόμενου τραπεζιού, το οποίο συνεργάζεται με το λογισμικό του σαρωτή και του επιτρέπει να γνωρίζει τις θέσεις των τμηματικών σαρώσεων. Σε κάποιες περιπτώσεις το λογισμικό του σαρωτή χειρίζεται και ένα σύνολο από φωτιστικά σώματα που σκοπό έχουν να δημιουργήσουν τις κατάλληλες συνθήκες φωτισμού για την καλύτερη αποτύπωση των δεδομένων επιφανειακής υφής του αντικειμένου.

Τις περισσότερες φορές μια σάρωση περιέχει κενά λόγω αδυναμίας άμεσης οπτικής επαφής του οπτικού συστήματος του σαρωτή με συγκεκριμένες περιοχές της επιφάνειας του αντικειμένου. Συχνά όμως εμφανίζονται και τμήματα σαρώσεων με διαφορετική πυκνότητα δεδομένων. Αυτό οφείλεται στην ανάγκη αλλαγής των ρυθμίσεων του σαρωτή, ώστε να αποδίδει καλύτερα σε περιπτώσεις όπου επιβάλλεται η μεταβολή απόστασης του από το αντικείμενο. Το φαινόμενο αυτό είναι πιο συνηθισμένο σε σαρωτές μεγάλου βεληνεκούς που χρησιμοποιούνται κατά κόρο στην αποτύπωση χώρων και κτηρίων. Ως εκτούτου το πλήθος των τμηματικών σαρώσεων καθορίζει την ολοκληρωμένη και ομοιογενή αποτύπωση των δεδομένων. Ο αυτόματος καθορισμός των καλύτερων οπτικών γωνιών για ψηφιοποίηση είναι επίσης ένα δύσκολο πρόβλημα. Η απλούστερη προσέγγιση στην επίλυση αυτού του προβλήματος είναι η χειροκίνητη επιλογή οπτικών γωνιών. Η ψηφιοποίηση θα πρέπει να πραγματοποιείται έχοντας πάντα υπόψη την ελαχιστοποίηση των διαφορετικών σαρώσεων αλλά και την εξασφάλιση ύπαρξης ενός μεγάλου ποσοστού επικαλυπτόμενων σημείων ανάμεσα στις διαφορετικές σαρώσεις.

Πολλοί είναι οι λόγοι που οδηγούν στην πραγματοποίηση σάρωσης με μέγιστη δυνατή ακρίβεια στην περίπτωση εργασιών σάρωσης πολιτιστικών αντικειμένων. Ένας από αυτούς βασίζεται στην αισιόδοξη ιδέα απόκτησης καλύτερων αποτελεσμάτων από τα ίδια δεδομένα. Η αισιοδοξία κρύβεται στο γεγονός ότι καθώς στο μέλλον θα αναπτυχθούν καλύτεροι αλγόριθμοι επεξεργασίας δεν θα απαιτηθεί η επανάληψη της διαδικασίας σάρωσης.

 

Προ-επεξεργασία γεωμετρικής πληροφορίας

Η διαδικασία της προ-επεξεργασίας πραγματοποιείται αμέσως μετά την αποτύπωση των δεδομένων γεωμετρίας και περιλαμβάνει ένα σύνολο από μερικώς ασυσχέτιστες εργασίες [82]. Είναι μια διαδικασία που συναντούμε συχνάστα σε εμπορικά συστήματα ως ενσωματωμένη μέσα στη διαδικασία δημιουργίας πολυγωνικών πλεγμάτων. Ο υπολογισμός των πινάκων καθέτων διανυσμάτων είναι μια από αυτές, κατά την οποία χρησιμοποιείται η γεωμετρική πληροφορία της σάρωσης για να αναγνωριστεί η φορά των διανυσμάτων αυτών για κάθε σημείο. Αυτή είναι πολύ σημαντική πληροφορία, η οποία μπορεί να χρησιμοποιηθεί αργότερα για την ορθή οπτική αναπαράσταση του αντικειμένου, την ενοποίηση τμημάτων αλλά και την τμηματοποίηση των δεδομένων.

 

Φιλτράρισμα του θορύβου στο νέφους σημείων

Τα δεδομένα που αποκτώνται από τους τρισδιάστατους σαρωτές περιέχουν, συνήθως, σφάλματα εξαιτίας της ύπαρξης θορύβου. Πολλοί ερευνητές έχουν μελετήσει τα σφάλματα αυτά. Ο θόρυβος εμφανίζεται με τη μορφή τυχαίων σημείων γύρω από την πραγματική επιφάνεια του αντικειμένου. Μια μέθοδος που επιτρέπει την απαλοιφή του θορύβου είναι ο υπολογισμός του μέσου όρου θέσης των σημείων ανάμεσα σε επικαλυπτόμενες σαρώσεις [68]. Άλλη μια τεχνική βασίζεται στην υπό-δειγματοληψία των σημείων του νέφους που πραγματοποιείται βάσει μιας εκτίμησης της επιφάνειας του αντικειμένου. Οι Alexa et al. [69] και Correa et al. [70] εφαρμόζουν την τεχνική Moving Least Square projection (MLS) του Levin [71] για να φιλτράρουν το θόρυβο. Ένα πλήθος αλγορίθμων που προέρχόνται από το χώρο της ψηφιακής επεξεργασίας εικόνας ομαλοποιούν τα δεδομένα του νέφους σε δύο διαστάσεις. Οι απλοί γραμμικοί αλγόριθμοι (π.χ.Gaussian smoothing) έχουν το μειονέκτημα να μην μπορούν να ξεχωρίσουν το θόρυβο από τα υψηλής συχνότητας δεδομένα. Έτσι καταλήγουν να ομαλοποιούν τις άκρες και τις λεπτομέρειες των αντικειμένων.Γενικότερα οι μη-γραμμικοί αλγόριθμοι είναι καταλληλότεροι για αφαίρεση του θορύβου [82]. Στην Εικόνα 59 παρουσιάζεται ένα παράδειγμα ομαλοποίησης νέφους σημείων για ένα σχετικά απλό αντικείμενο πολιτιστικής κληρονομιάς.

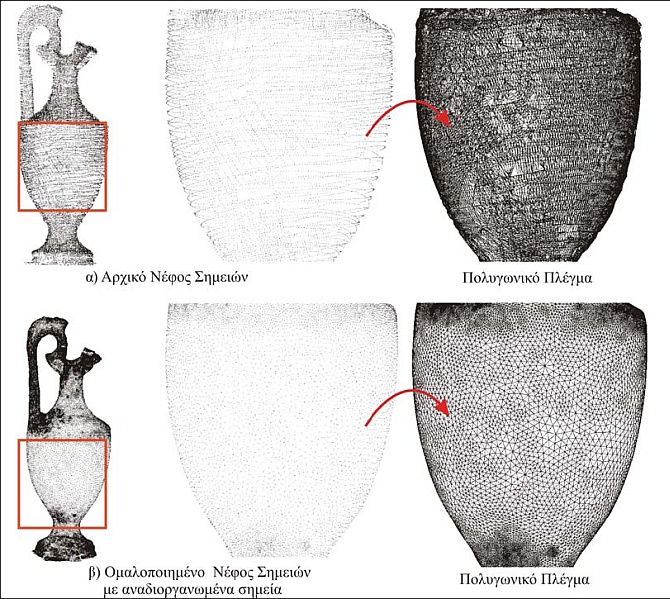
Εικόνα 59. Ομαλοποίηση νέφους σημείων

 

 

Ομαδοποίηση και οργάνωση των δεδομένων

Η διαχείριση του μεγάλου όγκου δεδομένων που παράγουν οι σαρωτές είναι ένα από τα βασικότερα προβλήματα κατά την διάρκεια της επεξεργασίας. Το μέγεθος των δεδομένων οδηγεί τα υπολογιστικά συστήματα στα όρια λειτουργίας τους, ιδιαίτερα όταν απαιτείται αλληλεπίδραση με τον χρήστη σε πραγματικό χρόνο. Η διαδικασία της ομαδοποίησης των δεδομένων αποτελεί μια λύση στο πρόβλημα. Ειδικές δομές δεδομένων (οκταδικά και δυαδικά δέντρα) οργανώνουν με τέτοιο τρόπο τα δεδομένα, ώστε η προσπέλαση τους να γίνεται έξυπνα και γρήγορα ανάλογα με την οπτική γωνία υπό την οποία εμφανίζεται το αντικείμενο. Οι δομές αυτές επιτρέπουν τη μερική εμφάνιση των δεδομένων και προσφέρουν την δυνατότητα επεξεργασίας σε πραγματικό χρόνο χωρίς την ανάγκη ταυτόχρονης προσπέλασης όλου του όγκου πληροφορίας [82].

 

Ευθυγράμμιση και ενοποίηση των τμηματικών σαρώσεων

Οι τμηματικές σαρώσεις πρέπει να ευθυγραμμισθούν μεταξύ τους έτσι ώστε να μπορεί να σχηματιστεί η πλήρης γεωμετρική απόδοση του αντικειμένου. Η διαδικασία αυτή μπορεί να είναι εξ' ολοκλήρου αυτοματοποιημένη εάν είναι γνωστή στο λογισμικό η θέση του σαρωτή σε κάθε τμηματική σάρωση. Όταν κάτι τέτοιο δεν ισχύει, η διαδικασία πρέπει να γίνει, αρχικά τουλάχιστον, χειροκίνητα. Ο χρήστης τοποθετεί με τη βοήθεια του λογισμικού τα τμήματα σε κάποιες θέσεις, οι οποίες θα βελτιωθούν στη συνέχεια αυτόματα από το ίδιο το λογισμικό. Ο χρήστης συνήθως ορίζει κάποια κοινά σημεία πάνω στις τμηματικές σαρώσεις, τα οποία θα χρησιμοποιήσει το λογισμικό για να τις ευθυγραμμίσει. Πάντως, τα περισσότερα συστήματα, σήμερα, βασίζονται στην ανθρώπινη παρέμβαση. Για τον λόγο αυτό έχουν αναπτυχθεί εύχρηστα διαδραστικά εργαλεία που υποβοηθούν με τη δυνατότητα άμεσης επιλογής χαρακτηριστικών ανάμεσα στις τμηματικές σαρώσεις. Το λογισμικό βασίζεται στα σημεία που θα του δώσει ο χρήστης για να δημιουργήσει τους κατάλληλους χωρικούς μετασχηματισμούς που θα αποφέρουν την ευθυγράμμιση των τμημάτων. Η χειροκίνητη ευθυγράμμιση απαιτεί αρκετό χρόνο, ίσως τον περισσότερο από όλα τα υπόλοιπα στάδια επεξεργασίας των δεδομένων. Η αυτοματοποιημένη εξακρίβωση των χαρακτηριστικών ανάμεσα στις τμηματικές σαρώσεις είναι μια επιθυμητή αλλά ταυτόχρονα δύσκολη διαδικασία. Αποτελεί, άλλωστε, ενεργό χώρο μελέτης και έρευνας.

Όταν το πλήθος των τμηματικών σαρώσεων αγγίζει τις αρκετές δεκάδες τότε η ευθυγράμμιση θα πρέπει να γίνεται σε επίπεδο ομάδων. Οι ομάδες ορίζονται συνήθως από το χρήστη. Γενικά, η ευθυγράμμιση τμηματικών σαρώσεων πραγματοποιείται ευκολότερα σε κλειστά αντικείμενα (π.χ. ένα βάζο) από ότι σε ανοικτά (π.χ. μια μαρμάρινη ανάγλυφη διακόσμηση) [7].

Ο αλγόριθμος επαναληπτικής προσέγγισης σημείου (ICP) έχει γίνει από όλους αποδεκτός ως η πιο χρήσιμη μέθοδος για ενοποίηση δεδομένων από διαφορετικά νέφη σημείων. Η πρώτη περιγραφή του αλγορίθμου έγινε από τους Besl και McKay το 1992 [8]. Ο αλγόριθμος πραγματοποιείται σε δύο διακριτά βήματα: κατά το πρώτο βήμα πραγματοποιείται η αναγνώριση αντίστοιχων σημείων, ενώ κατά το δεύτερο γίνεται εκτίμηση του χωρικού μετασχηματισμού που θα ελαχιστοποιήσει την απόσταση ανάμεσα τους. Η εκτέλεση των δύο αυτών βημάτων επαναλαμβάνεται μέχρι να επιτευχθεί το καλύτερο δυνατό συνταίριασμα. Ωστόσο βασικό του μειονέκτημα είναι η αστάθεια που παρουσιάζει σε ομαλές επιφάνειες.

Άλλες μέθοδοι ευθυγράμμισης βασίζονται σε κάποια ειδικά αντικείμενα έλεγχου (π.χ. σφαίρες, κυλίνδρους και επίπεδα). Τα αντικείμενα ελέγχου τοποθετούνται γύρω από το αντικείμενο προς ψηφιοποίηση. Τα αντικείμενα ελέγχου ψηφιοποιούνται μαζί με το αντικείμενο και μπορούν να αναγνωριστούν αυτόματα από το λογισμικό, το οποίο, αναγνωρίζοντας τη θέση τους, ευθυγραμμίζει τις τμηματικές σαρώσεις [95]. Το μειονέκτημα στη συγκεκριμένη περίπτωση είναι πως σε κάθε σάρωση θα πρέπει να εμφανίζονται τουλάχιστον τρία από τα αντικείμενα ελέγχου.

Μετά την ευθυγράμμιση των τμηματικών σαρώσεων, σειρά έχει η συγχώνευση και ενοποίησή τους (Εικόνα 60). Είναι η πλέον απαιτητική διαδικασία σε επίπεδο πόρων για ένα υπολογιστικό σύστημα. Πολλές φορές οι ίδιες οι εταιρείες ανάπτυξης του λογισμικού προτείνουν τον έλεγχο των διαθέσιμων υπολογιστικών πόρων, αφού ο όγκος των δεδομένων υπερβαίνει κατά πολύ την χωρητικότητα της μνήμης ενός απλού υπολογιστή.

Κατ τη διαδικασία ενοποίησης, το λογισμικό αναλαμβάνει να αφαιρέσει τα πλεονάζοντα σημεία που έχουν παραχθεί στα επικαλυπτόμενα τμήματα των σαρώσεων.Η ενοποίηση μπορεί να πραγματοποιηθεί σε διαφορετικά επίπεδα:

• Σε επίπεδο σημείων, αμέσως μετά την ευθυγράμμιση των τμημάτων: το λογισμικό εξετάζει εάν κάποιο σημείο μιας σάρωσης εμφανίζεται και σε κάποια άλλη σάρωση, και δεν το λαμβάνει στο εξής υπόψιν
• Σε επίπεδο περιοχής-αντικειμένου: καθώς τα δεδομένα μοντελοποιούνται, τα τμήματα που αναγνωρίζονται ως κοινά συγχωνεύονται
• Άμεση αναγνώριση: η αναγνώριση των σημείων γίνεται άμεσα πάνω σε ένα νέφος σημείων που αποτελείται από όλες τις τμηματικές σαρώσεις.Η μοντελοποίηση πάνω στο τρισδιάστατο νέφος σημείων είναι δύσκολη και απαιτεί μεγάλη υπολογιστική ισχύ.

Εικόνα 60. Ενοποίηση τμηματικών σαρώσεων

 

Δημιουργία πολυγωνικού πλέγματος (meshing)

Η διαδικασία αυτή αποτελεί τον πιο αντιπροσωπευτικό και ευρέως διαδεδομένο αλγόριθμο οπτικής αναπαράστασης τρισδιάστατων επιφανειών. Υπάρχουν διάφοροι αλγόριθμοι τριγωνοποίησης που έχουν ως κοινό στόχο τη μετατροπή ενός νέφους σημείων σε μια συνεχόμενη επιφάνεια από τρίγωνα (γνωστή και ως πολυγωνικό πλέγμα). Το πολυγωνικό πλέγμα αποτελεί μια πιο «διαισθητική» απόδοση του αντικειμένου, ιδιαίτερα όταν εφαρμοστεί πάνω του η πληροφορία υφής. Σημαντικό πλεονέκτημα της χρήσης πολυγωνικών πλεγμάτων είναι η σημαντική μείωση του όγκου δεδομένων που απαιτείται για την περιγραφή τρισδιάστατης γεωμετρίας. Το πολυγωνικό πλέγμα επιτρέπει τη διαδραστική μελέτη του τρισδιάστατου αντικείμενου για εξαγωγή διαστάσεων, ορθογραφικών φωτογραφιών, κ.α. Ορισμένοι αλγόριθμοι [96],[97] υπολογίζουν το πλέγμα προοδευτικά, βασιζόμενοι στην πληροφορία που παρέχουν τα γειτονικά σημεία του νέφους. Άλλοι, πιο πολύπλοκοι, αποφασίζουν και για την ανάλυση του πλέγματος σε κάθε περιοχή ανάλογα με τα χαρακτηριστικά των επιφανειών που δημιουργούν (καμπύλες και επίπεδα).

Ένα σημαντικό πρόβλημα είναι ότι ο θόρυβος που έχει καταφέρει να διαφύγει από το αρχικό φιλτράρισμα του νέφους εμφανίζεται πιο έντονος στις επιφάνειες του τριγωνικού πλέγματος.

 

Απλοποίηση του πολυγωνικού πλέγματος

Όπως έχει ήδη επισημανθεί, η μείωση της γεωμετρικής πληροφορίας είναι απαραίτητη για την αποτελεσματική διαχείριση των τρισδιάστατων μοντέλων. Η απλοποίηση της γεωμετρίας πραγματοποιείται σε περιοχές της επιφάνειας του αντικειμένου που δεν παρουσιάζουν έντονες μεταβολές. Ένας ρυθμός δειγματοληψίας της τάξης των 0,22 χιλιοστών για μια επίπεδη επιφάνεια, αποδεικνύεται μάλλον άστοχος, αφού κάτω από συγκεκριμένες συνθήκες, η ίδια επιφάνεια θα μπορούσε να περιγραφεί από ελάχιστα σημεία. Οι σύγχρονοι αλγόριθμοι απλοποίησης γεωμετρίας αναγνωρίζουν αυτόματα τα τμήματα ενός τρισδιάστατου μοντέλου που μπορούν να υποστούν απλοποίηση χωρίς να υποβαθμιστεί η ποιότητα τους [98],[99]. Ειδικές δομές δεδομένων διαχωρίζουν τη γεωμετρία του μοντέλου σε τμήματα. Ο διαχωρισμός γίνεται με κριτήριο την πολυμορφία της επιφάνειας ανάλογα με την περιοχή. Η οργάνωση των δεδομένων κατά αυτό τον τρόπο συνεισφέρει στην αφαίρεση πληροφορίας ανάλογα με τις ανάγκες της κάθε περιοχής.

Χαρακτηριστικό είναι το παράδειγμα της ομάδας που εργάστηκε στην ψηφιοποίηση του Δαβίδ του Michelangelo (Digital Michelangelo Project). Η ερευνητική ομάδα ανέπτυξε έναν αλγόριθμο που βασίζεται στην τεχνική της εικονικής μνήμης και καταφέρνει να επεξεργαστεί και να απλοποιήσει μοντέλα με εντυπωσιακά αποτελέσματα. Στην συγκεκριμένη περίπτωση το αρχικό μοντέλο του Δαβίδ έφερε 2 δισεκατομμύρια τρίγωνα, τα οποία μειώθηκαν σε μόλις 56 εκατομμύρια.

Σε κάποιες περιπτώσεις η απλοποίηση μπορεί να θεωρηθεί απλά μια προσπάθεια συμβιβασμού ανάμεσα στην ποιότητα του τρισδιάστατου μοντέλου και του όγκου δεδομένων που το περιγράφει. Με την εφαρμογή ενός αλγορίθμου απλοποίησης η απώλεια πληροφορίας είναι, προφανώς, αναπόφευκτη.

Ο παρακάτω πίνακας συνοψίζει τις μειώσεις που δέχεται ένα τρισδιάστατο μοντέλο, που προέρχεται από αρχικό πολυγωνικό πλέγμα 34.970 τριγώνων, υπό την επίδραση διαφόρων μεθόδων απλοποίησης γεωμετρίας. Οι αλγόριθμοι που συγκρίνονται είναι οι Quadric Error, Quadric Error Weighted [100], απλοποίησητου Stan Melax [101] και ένας απλός αλγόριθμος που αφαιρεί σε κάθε εκτέλεσητου τις μικρότερες σε μήκος τριγωνικές πλευρές [102]. Το πολυγωνικό πλέγμα απλοποιείται με σταθερό ποσοστιαίο βήμα ενώ τα αποτελέσματα που περιέχει ο πίνακας ανταποκρίνονται στο τελικό πλήθος των τριγώνων του πλέγματος. Ας σημειωθεί ότι η απλοποίηση εφαρμόζεται στο αρχικό γεωμετρικό πλέγμα.

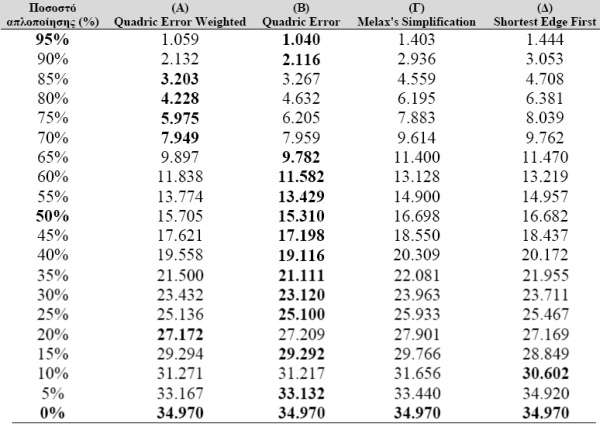Σύγκριση αποτελεσμάτων αλγορίθμων απλοποίησης γεωμετρίας

Ενδιάμεσα στάδια διαδικασιών παρουσιάζονται στις εικόνες που ακολουθούν (Εικόνα 61, Εικόνα 62). Χαρακτηριστικό φαινόμενο είναι η εμφάνιση κενών (ασυνέχειες στο πολυγωνικό πλέγμα) στις απλοποιημένες εκδόσεις της γεωμετρίας. Αυτό γίνεται ιδιαίτερα εμφανές στον αλγόριθμο (Δ) όπου τα κενά εμφανίζονται πολύ νωρίς (πολύ πιο πριν από τις άλλες μεθόδους).

Κάποια βασικά χαρακτηριστικά που θα μπορούσαν να χρησιμοποιηθούν ως κριτήρια αξιολόγησης ενός αλγορίθμου απλοποίησης γεωμετρίας είναι τα παρακάτω [100]:

• Αποτελεσματικότητα: η ικανότητα του αλγόριθμου να απλοποιεί με γρήγορους ρυθμούς σύνθετα μοντέλα
• Ποιότητα: οι προσεγγίσεις που προκύπτουν από τον αλγόριθμο διατηρούν την υψηλότερη δυνατή πιστότητα των λεπτομερειών του αρχικού μοντέλου
• Γενικότητα: η αναμενόμενη παρόμοια συμπεριφορά του αλγορίθμου κάτω από οποιεσδήποτε πιθανές μορφές επιφάνειας.

 

 

 

 

 

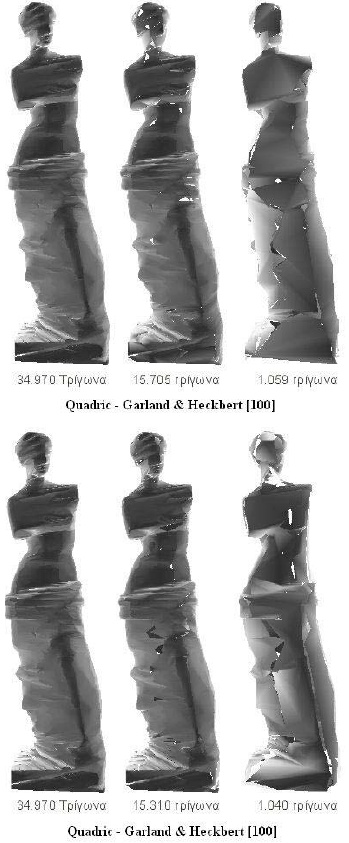
Εικόνα 62. Αλγόριθμοι απλοποίησης

 

Απαλοιφή γεωμετρικών ασυνεχειών

Σε ομαλές ή επίπεδες επιφάνειες η συμπλήρωση των κενών μπορεί να πραγματοποιηθεί με μια απλή διαδικασία παρεμβολής (interpolation). Οι Wangκαι Oliveira [72] περιγράφουν μια διαδικασία για την αυτόματη αναγνώριση γεωμετρικών ασυνεχειών και της απαλοιφής τους. Τα κενά αναγνωρίζονται αναλύοντας το τριγωνικό πλέγμα σε κυκλική φορά, ενώ, ταυτόχρονα, πραγματοποιείται αναζήτηση για μη κοινές πλευρές (Εικόνα 63). Ο συγκεκριμένος αλγόριθμος δε δύναται να αναγνωρίσει τα σημεία της επιφάνειας όπου πραγματικά υπάρχει ασυνέχεια. Επίσης δεν αντιλαμβάνεται τις περιοχές που πάσχουν από υπόδειγματοληψία (αραιά τοποθετημένα τρίγωνα). Σε αυτές τις περιπτώσεις απαιτείται η συμμετοχή του χρήστη. Μόλις αναγνωριστεί το κενό δημιουργούνται τα ενδιάμεσα σημεία βάσει των γειτονικών τους. Τα τρίγωνα που εμφανίζονται χρωματισμένα με γκρι σκούρο χρώμα στην Εικόνα 63 αποτελούν τα συμφραζόμενα παρεμβολής, πάνω στα οποία βασίζεται ο αλγόριθμος για να γεμίσει το κενό.

 

 

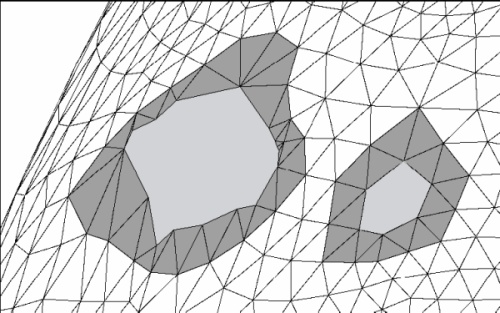
Εικόνα 63. Αναγνώριση ασυνεχειών σε τριγωνικό πλέγμα

 

Αν και υπάρχουν αρκετές και διαφορετικές τεχνικές απαλοιφής ασυνεχειών, τα αποτελέσματα τους, τις περισσότερες φορές, δε συμβαδίζουν με την πληροφορία που φέρουν τα πραγματικά αντικείμενα. Παρόλα αυτά, όμως, αποτελούν τη μοναδική λύση αντιμετώπισης του συγκεκριμένου προβλήματος.

Μια εναλλακτική τεχνική για τη συμπλήρωση κενών σε νέφη σημείων έχει προταθεί από τους Carr et al.[73]. Η τεχνική αυτή χρησιμοποιεί πολύ-αρμονικές πολικές συναρτήσεις. Μπορεί και διαχειρίζεται μεγάλους όγκους δεδομένων και παράγει εντυπωσιακά αποτελέσματα. Μπορεί επίσης να χρησιμοποιηθεί και ως τεχνική τμηματοποίησης και αναδιοργάνωσης νεφών σημείων.

 

Δημιουργία υφής

Σε εφαρμογές αντίστροφης μηχανικής, η χρωματική πληροφορία υφής των αντικειμένων που ψηφιοποιούνται δεν είναι απαραίτητη και αποτελεί πλεονασμό. Η συγκεκριμένη άποψη έρχεται σε αντίθεση με τις ανάγκες ψηφιοποίησης των πολιτισμικών αντικειμένων. Η πληροφορία υφής προσδίδει στο αντικείμενο φωτορεαλισμό. Μεγάλο τμήμα της πληροφορίας που φέρουν τα πολιτιστικά αντικείμενα βρίσκεται αποτυπωμένο στην υφή τους. Πάμπολλες είναι, για παράδειγμα, οι περιπτώσεις στις οποίες η διακόσμηση ενός αρχαιολογικού ευρήματος φέρει ζωτικής σημασίας πληροφορία για έναν αρχαιολόγο.

Η τεχνητή ανακατασκευή της όψης ενός αντικειμένου είναι ένα από τα τελευταία στάδια της διαδικασίας ψηφιοποίησης. Πολλές εφαρμοσμένες τεχνικές προβάλουν, άμεσα, φωτογραφίες πάνω στη γεωμετρία του αντικειμένου για να δημιουργήσουν τους λεγόμενους χάρτες υφής (texture maps) (Εικόνα 64).Διαφορετικές εικόνες συγχωνεύονται για τη δημιουργία του τελικού χάρτη υφής. Η συγχώνευση αυτή πραγματοποιείται με τη χρήση κάποιων τεχνικών ανάμιξης των χρωμάτων ανάμεσα στα όρια των εικόνων (βλέπε Σχήμα-Από-Σιλουέτες). Εκτός από το μεγάλο πλεονέκτημα της ρεαλιστικής απόδοσης του αντικειμένου, η συγκεκριμένη μεθοδολογία παρουσιάζει κάποια προβλήματα. Η πληροφορία υφής του αντικειμένου εμφανίζεται κάτω από συγκεκριμένες συνθήκες φωτισμού, οι οποίοι είναι, πολλές φορές, απαγορευτικοί για διαδικασίες φωτορεαλιστικής απόδοσης. Με άλλα λόγια, το αντικείμενο εμφανίζεται πάντα στις συνθήκες φωτισμού που περιέχουν οι φωτογραφίες που χρησιμοποιήθηκαν ως βάση για την δημιουργία του τελικού χάρτη υφής. Γι' αυτόν ακριβώς το λόγο, έχουν πραγματοποιηθεί πάμπολλες μελέτες για την παραγωγή χαρτών υφής ανεξαρτήτως συνθηκών φωτισμού [9]-[11].

 

 

 

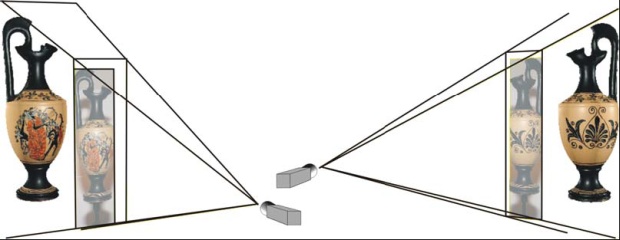
Εικόνα 64. Προβολή εικόνων πάνω στο πολυγωνικό πλέγμα

 

Τέλος, θα πρέπει να αναφερθεί ότι, εκτός από την ανακατασκευή γεωμετρίας στα σημεία όπου υπάρχουν κενά, κάποιες φορές, είναι απαραίτητη και η ανακατασκευή της πληροφορίας υφής. Η διαδικασία των moving-least-squares μπορεί να εφαρμοστεί για την ανακατασκευή τεχνητών ομαλά μεταβαλλόμενων χρωμάτων. Αυτό επιτυγχάνεται με την αντικατάσταση της χρωματικής τιμής ενός εικονοστοιχείου ανάλογα με τις τιμές που έχει η γεωμετρία στον άξονα Ζ στο συγκεκριμένο σημείο και με την πληροφορία από τα γειτονικά εικονοστοιχεία.